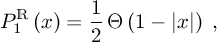Statistics of Φ’s Eigenvalues [5]

When analyzing the statistic of the N^R REAL eigenvalues of Φ, the very same concentration effect of Fig. (2) has been found, so that the rescaling of eq. (6) has to be taken in account here too.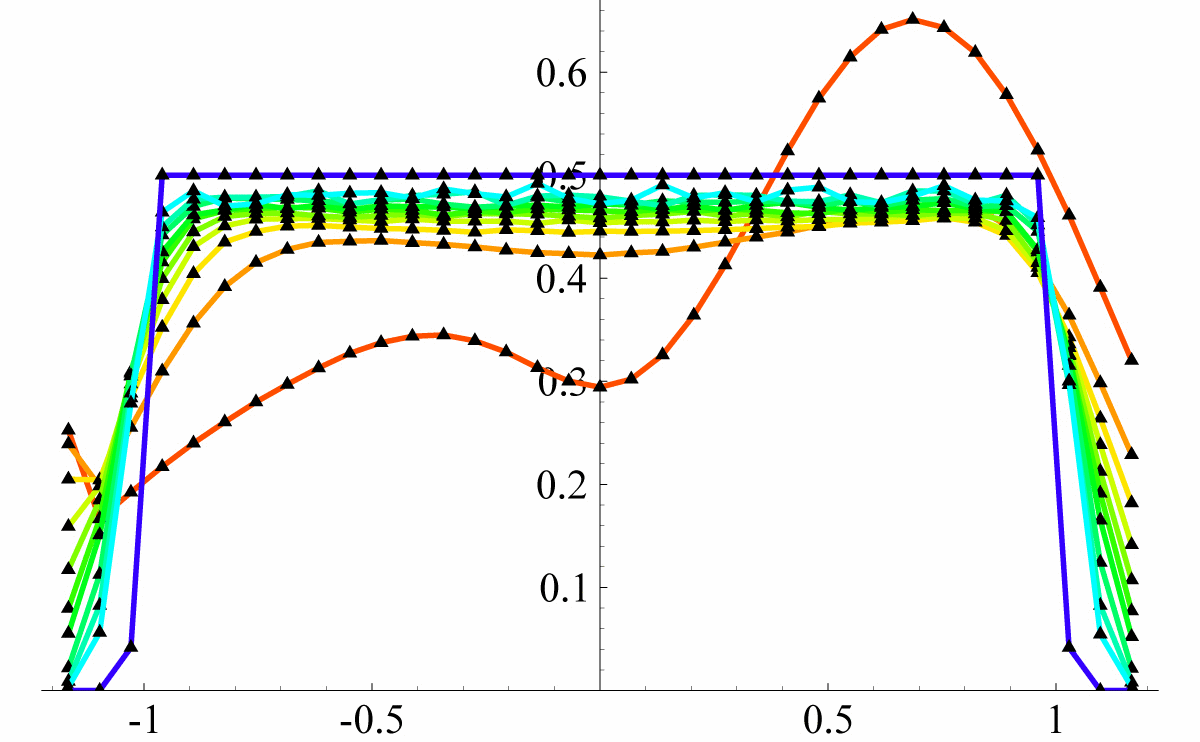

The statistics of such N^R REAL eigenvalues of Φ is the argument of the next fig. (4).

Figure 4: Histograms of Φ’s Eigenvalues

This plot represents a bunch of 11 histograms of the REAL eigenvalues of rescaled superoperators Φ, distributed according to the measure induced by running the Hans-Jürgen procedure. The different colored lines represent the cases N=2 (two non-equal bumps − red line), N=3,4,5,6,7,8,10,12 and N=14 (light-blue line). Finally, we plotted in dark-blue the step function,

that we expect to represent the limiting distribution for very large N.

The domain [-1.2,1.2] has been divided into 35 segment, frequency count in the 35 bins has been performed, and the probability histograms P^R₁ (x) have been obtained by rescaling.

For what computational time is concerned, have a look in table. (1).

2.3. Distribution of the REAL Φ’s Eigenvalues