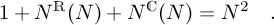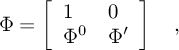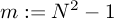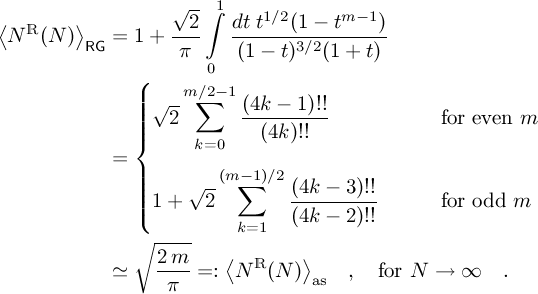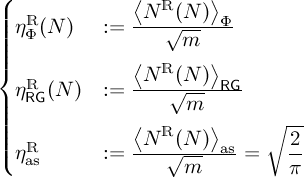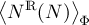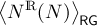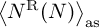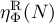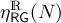|
As D is positive and hermitian, its eigenvalues are positive and
REAL. Conversely, Φ’s eigenvalues are generally CPLX.
Namely that, on average, for a single N2×N2
superoperator Φ, its N2 eigenvalues can be classified in
three family:
- One simple eigenvalue equal to +1 ;
- NR(N) REAL eigenvalues from the open interval (-1,+1) ;
- NC(N) CPLX eigenvalues from the interior of the unit
circle |z|<1 .
Of course the following balance equation has to be fulfilled:
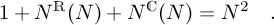 (3)
(3)
In the next table. (1) we display the outcome
of a simulation. We generate a certain number M of
N2−dimensional superoperator Φ according to the
Hans-Jürgen algorithm, and we diagonalize them, listing the
number of eigenvalues falling into the three families of the very previous list.
Of course # ALL = M N2 ; # 1 = M ; # REAL = M NR(N) and # CPLX = M NC(N) .
| N |
N2 |
M :
Number of
matrices |
Eigenvalues’s Counting |
Comp.
Time
(hours) |
| # ALL |
# 1 |
# REAL |
# CPLX |
|
|
4 |
9 |
16 |
25 |
36 |
49 |
64 |
100 |
144 |
196 |
|
90000000 |
17000000 |
4200000 |
1300000 |
500000 |
210000 |
90000 |
75000 |
27000 |
9000 |
|
360000000 |
153000000 |
67200000 |
32500000 |
18000000 |
10290000 |
5760000 |
7500000 |
3888000 |
1764000 |
|
90000000 |
17000000 |
4200000 |
1300000 |
500000 |
210000 |
90000 |
75000 |
27000 |
9000 |
|
139221060 |
45132048 |
14795938 |
5660628 |
2587686 |
1257274 |
610722 |
630110 |
269494 |
104478 |
|
130778940 |
90867952 |
48204062 |
25539372 |
14912314 |
8822726 |
5059278 |
6794890 |
3591506 |
1650522 |
|
|
Table 1: Eigenvalues’s Counting
The number of matrices that has been used varies. Namely that it has
been determined has a good compromise between smoothness of the
3-dimensional surfaces of fig. (2) and fig. (3)
and the computational time, displayed in the last column.
Once the dimension N has been chosen,
eq. (3) make it apparent how just one parameter
is neded, for instance NR(N), for completely determine all the
quantities.
The N2xN2 superoperator Φ can be decomposed as
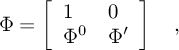
where the (N2−1)−dimensional vector Φ0
represent a translation while the (N2−1)x(N2−1)
dimensional matrix Φ’ represent a real antisymmetric
contraction. Thus, the statistics of Φ is determined by the
statistics of Φ’, which contains the
NR(N) REAL and the NC(N) CPLX eigenvalues
different from +1.
We now fix
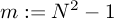
and make our ansatz:
|
We believe that the statistics of
eigenvalues of very large m x m real antisymmetric
contraction Φ’ embedded in a
superoperator Φ tends eventually to
that of the REAL ginibre ensemble
GinOE(m),
the ensemble of
m x m REAL matrices whose
entries are normally distributed.
|
If it is so, at least for large N,
we can expect the scaling behavior of 〈NR(N)〉Φ ,
becomes that of
the average number
of eigenvalues in the REAL ginibre ensemble, hereafter
indicated with 〈NR(N)〉RG (although we are going to use expressions like 〈NR(N)〉RG, please, keep in mind relation between
m and N, given by m = N2 − 1).
From [Som07], [EK95] and [Ede97], we know the analytic expressions
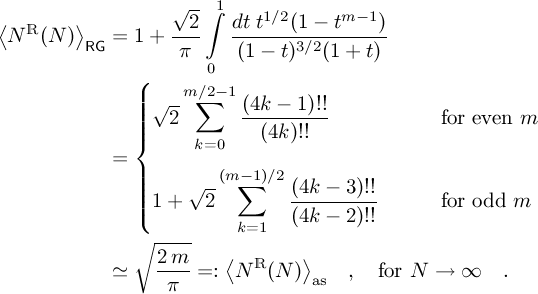
(4)
The latter symbol 〈NR(N)〉as denotes the asymptotic scaling of 〈NR(N)〉RG .
We now compute our numerical estimation of 〈NR(N)〉Φ from table. (1), simply considering the ratio 〈NR(N)〉Φ = # REAL / M ,
and compare such result with the analytical estimations of 〈NR(N)〉RG and 〈NR(N)〉as yielded by eq. (4).
Moreover we compute and display in table. (2) also the correspondent density
of REAL eigenvalues
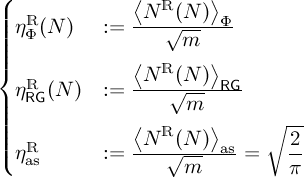
(5)
| N |
m |
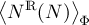 |
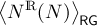 |
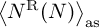 |
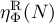 |
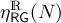 |
|
|
3 |
8 |
15 |
24 |
35 |
48 |
63 |
99 |
143 |
195 |
|
1.54690 |
2.65483 |
3.52284 |
4.35433 |
5.17537 |
5.98702 |
6.78580 |
8.40147 |
9.98126 |
11.60870 |
|
1.70711 |
2.65027 |
3.51264 |
4.34759 |
5.16969 |
5.98467 |
6.79528 |
8.40876 |
10.01628 |
11.62042 |
|
1.38198 |
2.25676 |
3.09019 |
3.90882 |
4.72035 |
5.52791 |
6.33301 |
7.93885 |
9.54131 |
11.14185 |
|
0.89310 |
0.93862 |
0.90959 |
0.88882 |
0.87480 |
0.86415 |
0.85493 |
0.84438 |
0.83467 |
0.83131 |
|
0.98560 |
0.93701 |
0.90696 |
0.88745 |
0.87384 |
0.86381 |
0.85612 |
0.84511 |
0.83760 |
0.83216 |
|
Table 2: Fraction of REAL eigenvalues
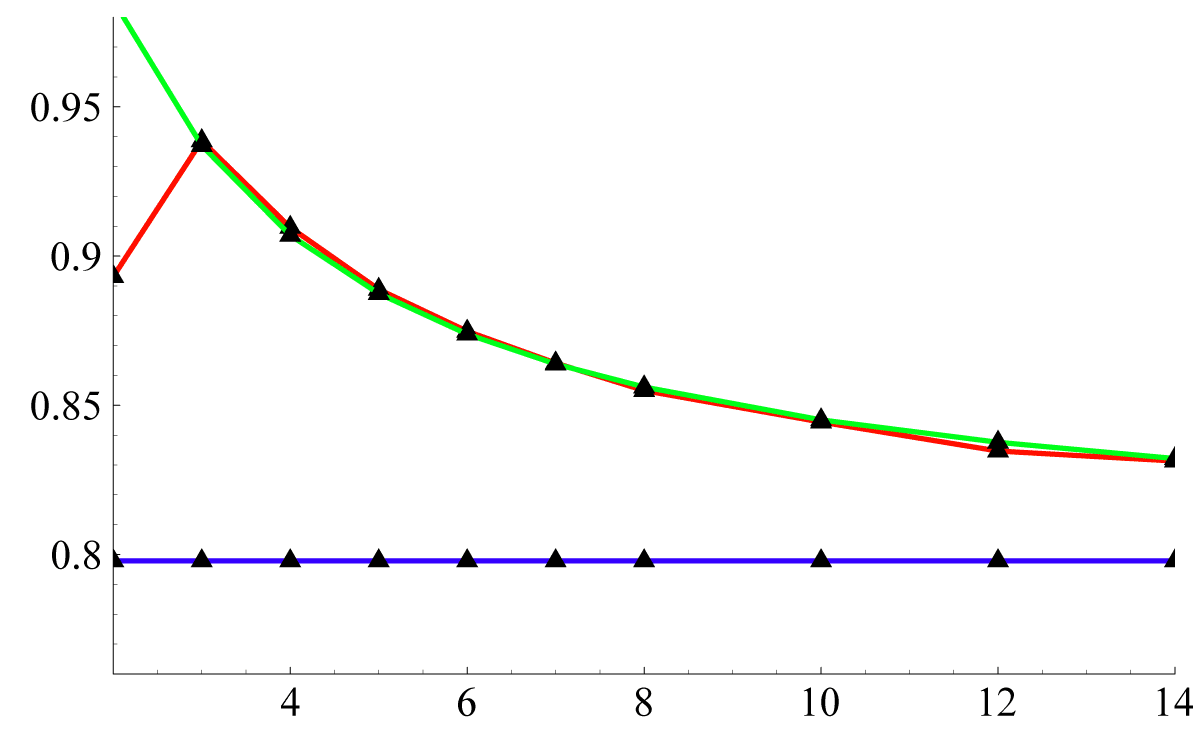
Finally, we plot in Fig. (1) the last
three column of table. (2).
Figure 1: Numerical, theoretical, and asymptotical ratios
This plot shows the asymptotical similarities of the ratio of
rescaled REAL eigenvalues for two cases:
- N2−dimensional superoperators Φ
(function ηRΦ(N), in red line);
- N2−dim. matrices from the REAL Ginibre ensemble
(ηRRG(N), in green line).
Moreover, both the 2 ratios do converge to the asymptote
η Ras ( blu
line), for eventually large N.
|