| | |
|
The subroutines listed in this Section are designed for performing the
operations of Table 1 on operators X,
mapping a finite dimensional bipartite Hilbert space
Htot = HA
⊗ HB =
CN
⊗ CK
into itself
X :
Htot →
Htot .
|
|
Table 1: Reshuffling Operations
Reorderings of a matrix X representing an operator which acts on a composed Hilbert space.
The arrows denote the indices exchanged.
|
|
All the subroutines linked on this pages incorporate the definitions described in the book
Ingemar Bengtsson and Karol Zyczkowski
Geometry of Quantum States
Cambridge University Press, Cambridge, 2006,
from which
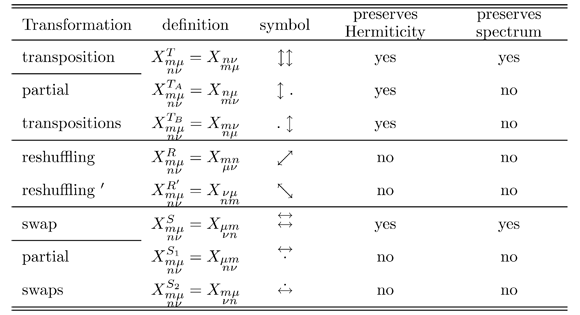
Table 1 is taken, and in the paper
Karol Zyczkowski and Ingemar Bengtsson
On duality between quantum maps and quantum states
Open Sys. Inf. Dyn. 11, 3-42 (2004).
In the latter reference the term “flip” is used in place of “swap”.
|
|
|
Some distinctions are in order:
- X can either be REAL or CPLX;
- in the input of the subroutine, X can either be expressed in
the “product
basis” of
CN
⊗ CK, namely
|m,μ〉 := |m〉A
⊗ |μ〉B , or in the “overall basis”
of
CNK, namely
|i〉tot .
According to the last of the points listed above, when X is given in the overall basis, it
will be considered as a 2-dimensional NK x NK matrix whose matrix elements X(i,j) are given by
X(i,j) = tot〈i| X
|j〉tot .
Conversely, when X is given in the product basis, it
will be considered as a 4-dimensional N x K x N x K matrix whose matrix elements X(m,μ,n,ν) are given by
X(m,μ,n,ν) = 〈m,μ| X
|n,ν〉 .
Conversion between the 2 basis are possible by means of 4 subroutines, called
R_NK_pro.f
,
C_NK_pro.f
,
R_pro_NK.f
,
C_pro_NK.f
and listed here below.
|
|
| |
| Subroutine ’s Name |
Precision |
Version |
Compatibility |
|
R_NK_pro.f |
Single |
1.0.0 |
Fortran 90 |
| Uses:
None
|
|
Description:
|
it take as input 2 INTEGER numbers N and K and a REAL
matrix X, whose matrix elements are given in the product basis of CN
⊗ CK; return as output the same matrix X,
but now expressed in the overall basis of CNK.
|
|
|
| |
| Subroutine ’s Name |
Precision |
Version |
Compatibility |
|
C_NK_pro.f |
Complex |
1.0.0 |
Fortran 90 |
| Uses:
None
|
|
Description:
|
it take as input 2 INTEGER numbers N and K and a CPLX
matrix X, whose matrix elements are given in the product basis of CN
⊗ CK; return as output the same matrix X,
but now expressed in the overall basis of CNK.
|
|
|
| |
| Subroutine ’s Name |
Precision |
Version |
Compatibility |
|
R_pro_NK.f |
Single |
1.0.0 |
Fortran 90 |
| Uses:
None
|
|
Description:
|
it take as input 2 INTEGER numbers N and K and a REAL
matrix X, whose matrix elements are given in the overall basis of CNK;
return as output the same matrix X, but now expressed in the product basis of CN
⊗ CK.
|
|
|
| |
| Subroutine ’s Name |
Precision |
Version |
Compatibility |
|
C_pro_NK.f |
Complex |
1.0.0 |
Fortran 90 |
| Uses:
None
|
|
Description:
|
it take as input 2 INTEGER numbers N and K and a CPLX
matrix X, whose matrix elements are given in the overall basis of CNK;
return as output the same matrix X, but now expressed in the product basis of CN
⊗ CK.
|
|
|
According to the fact that matrices X can either be expressed in both the two basis,
and moreover can either be REAL or CPLX, we divided the following 32 subroutines in 4 families:
- • REAL Matrices X given in the product basis [8]
-
|
This 8 subroutines act onto REAL matrices X as described in
Table 1.
Inputs/Outputs are given in the product basis of CN
⊗ CK.
|
- • CPLX Matrices X given in the product basis [8]
-
|
This 8 subroutines act onto CPLX matrices X as described in
Table 1.
Inputs/Outputs are given in the product basis of CN
⊗ CK.
|
- • REAL Matrices X given in the overall basis [8]
-
|
This 8 subroutines act onto REAL matrices X as described in
Table 1.
Inputs/Outputs are given in the overall basis of CNK.
|
- • CPLX Matrices X given in the overall basis [8]
-
|
This 8 subroutines act onto CPLX matrices X as described in
Table 1.
Inputs/Outputs are given in the overall basis of CNK.
|
|
|
