|
In the input of the subroutines listed here below, X is expressed in
the “product basis” of the Hilbert space
of equation (1),
|m,μ〉 := |m〉A⊗ |μ〉B ,
as a 4-dimensional N x K x N x K matrix, whose elements X(m,μ,n,ν) are given by
X(m,μ,n,ν) = 〈m,μ| X
|n,ν〉 .
|
|
| Subroutine ’s Name |
Precision |
Version |
Compatibility |
|
C_NK_tot_tran.f |
Single |
1.0.0 |
Fortran 90 |
| Uses:
None
|
|
Description:
|
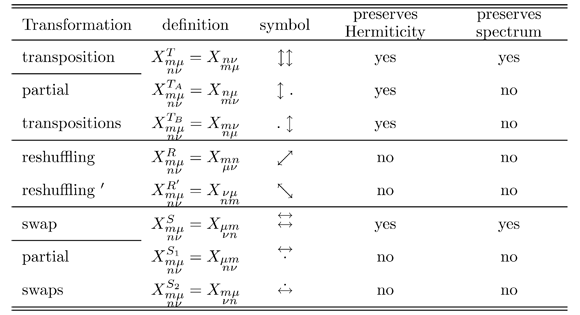
• Perform on a matrix X the operation [T] of Table 1.
• Input 2 INTEGER numbers N and K and the N x K x N x K CPLX
matrix X, whose matrix elements are given in the product basis of CN
⊗ CK.
• Return as output the N x K x N x K CPLX
matrix "total transpose of X", still expressed in the product basis of CN
⊗ CK.
|
|
|
| |
| Subroutine ’s Name |
Precision |
Version |
Compatibility |
|
C_NK_par_tr_A.f |
Single |
1.0.0 |
Fortran 90 |
| Uses:
None
|
|
Description:
|
• Perform on a matrix X the operation [TA] of Table 1.
• Input 2 INTEGER numbers N and K and the N x K x N x K CPLX
matrix X, whose matrix elements are given in the product basis of CN
⊗ CK.
• Return as output the N x K x N x K CPLX
matrix "partial transpose on A of X", still expressed in the product basis of CN
⊗ CK.
|
|
|
| |
| Subroutine ’s Name |
Precision |
Version |
Compatibility |
|
C_NK_par_tr_B.f |
Single |
1.0.0 |
Fortran 90 |
| Uses:
None
|
|
Description:
|
• Perform on a matrix X the operation [TB] of Table 1.
• Input 2 INTEGER numbers N and K and the N x K x N x K CPLX
matrix X, whose matrix elements are given in the product basis of CN
⊗ CK.
• Return as output the N x K x N x K CPLX
matrix "partial transpose on B of X", still expressed in the product basis of CN
⊗ CK.
|
|
|
| |
| Subroutine ’s Name |
Precision |
Version |
Compatibility |
|
C_NK_resh____.f |
Single |
1.0.0 |
Fortran 90 |
| Uses:
None
|
|
Description:
|
• Perform on a matrix X the operation [R] of Table 1.
• Input 2 INTEGER numbers N and K and the N x K x N x K CPLX
matrix X, whose matrix elements are given in the product basis of CN
⊗ CK.
• Return as output the N x N x K x K CPLX
matrix "reshuffling of X", in the basis of
(CN
⊗
CN)
⊗
(CK
⊗
CK)*.
|
|
|
| |
| Subroutine ’s Name |
Precision |
Version |
Compatibility |
|
C_NK_resh__pr.f |
Single |
1.0.0 |
Fortran 90 |
| Uses:
None
|
|
Description:
|
• Perform on a matrix X the operation [R’] of Table 1.
• Input 2 INTEGER numbers N and K and the N x K x N x K CPLX
matrix X, whose matrix elements are given in the product basis of CN
⊗ CK.
• Return as output the K x K x N x N CPLX
matrix "reshuffling’ of X", in the basis of
(CK
⊗
CK)
⊗
(CN
⊗
CN)*.
|
|
|
| |
| Subroutine ’s Name |
Precision |
Version |
Compatibility |
|
C_NK_tot_swap.f |
Single |
1.0.0 |
Fortran 90 |
| Uses:
None
|
|
Description:
|
• Perform on a matrix X the operation [S] of Table 1.
• Input 2 INTEGER numbers N and K and the N x K x N x K CPLX
matrix X, whose matrix elements are given in the product basis of CN
⊗ CK.
• Return as output the K x N x K x N CPLX
matrix "total swap of X", expressed in the product basis of CK
⊗ CN.
|
|
|
| |
| Subroutine ’s Name |
Precision |
Version |
Compatibility |
|
C_NK_par_sw_1.f |
Single |
1.0.0 |
Fortran 90 |
| Uses:
None
|
|
Description:
|
• Perform on a matrix X the operation [S1] of Table 1.
• Input 2 INTEGER numbers N and K and the N x K x N x K CPLX
matrix X, whose matrix elements are given in the product basis of CN
⊗ CK.
• Return as output the K x N x N x K CPLX
matrix "partial swap(1) of X", in the basis of
(CK
⊗
CN)
⊗
(CN
⊗
CK)*.
|
|
|
| |
| Subroutine ’s Name |
Precision |
Version |
Compatibility |
|
C_NK_par_sw_2.f |
Single |
1.0.0 |
Fortran 90 |
| Uses:
None
|
|
Description:
|
• Perform on a matrix X the operation [S2] of Table 1.
• Input 2 INTEGER numbers N and K and the N x K x N x K CPLX
matrix X, whose matrix elements are given in the product basis of CN
⊗ CK.
• Return as output the N x K x K x N CPLX
matrix "partial swap(2) of X", in the basis of
(CN
⊗
CK)
⊗
(CK
⊗
CN)*.
|
|
|
| |