Host community

One of the new aspects of the VECTRI model is that is explicitly allows the interaction between vector and host population on a district and regional scale. The VECTRI model specifies the population density using the Africa-only AFRIPOP [#!linard:12a!#] or global GRUMP [#!balk:06!#] datasets which have a nominal 1 km and 4.5 km spatial resolution, respectively. Thus at each location (model spatial grid cell), the ratio of biting vectors to hosts is known and is given by ( $\sum_{j=1}^{N_{sporo}} V(1,j)/H$ ). This is important to represent the vector-to-host transmission rate. The number of bites that any particular individual receives in a given time the human biting rate () is considered to be a random process, and thus distributed following a Poisson process with a mean biting rate of

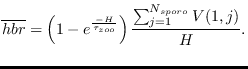$\displaystyle \overline{hbr}=\left( 1-e^{\frac{-H}{\tau_{zoo}}} \right) \frac{\sum^{N_{sporo}}_{j=1}{V(1,j)}}{H}.$

(12)

The factor $1-e^{\frac{-H}{\tau_{zoo}}}$ represents the level of vector zoophilly. While members of the Anopheles gambiae complex are in general considered anthropophilic to varying degrees [#!dekker:02!#], with arabiensis more zoophilic than sensu stricto [#!mahande:07!#], vectors take an increasing proportion of blood meals from cattle in lower population density rural areas with high livestock numbers [#!killeen:01!#], although the effectiveness of zooprophylaxis is still debated [#!bogh:01!#]. The exponential factor reflects this, with the e-folding population density for the effect set to $\tau_{zoo}$ =50 km $^{-2}$ . Thus the factor only has a significant impact for rural populations below this number and avoids the model producing excessively high biting rates and EIR for sparsely populated locations. In future, VECTRI will allow vector movement between cells allowing anthropophilic vectors to cluster around population centres.

The daily number of infectious bites by infectious vectors, , is the product of and the CircumSporozoite Protein Rate, . Specifically in the VECTRI notation, this is $V(1,N_{sporo})/H$ , with the indicating that the calculation is restricted to the vectors that are biting within the present timestep of the model. This implicitly assumes that there is no change in the intensity of biting or the gonotrophic cycle length between uninfected and infectious vectors; a simplification according to [#!koella:98!#]. If the transmission probability from vector to host for a single bite of an infective vector, $P_{vh}$ , is assumed a constant (VECTRI adopts a value of 0.3 [#!ermert:11a!#]) then the transmission probability for an individual receiving infectious bites will be $1-(1-P_{vh})^n$ . The impact on transmission due to blocking immunity is neglected. Thus the overall transmission probability per person per day in the model can be obtained by integration the over the bite distribution:

$\displaystyle P_{v{\rightarrow}h}= \sum_{n=1}^{\infty} G_{\overline{EIR_d}}(n)\left(1 - (1-P_{vh})^n \right)$

(13)

where $G_{\overline{EIR_d}}$ is the Poisson distribution for mean $\overline{EIR_d}$ . If bednets are in use, eqn.

could be modified to incorporate this, increasing the mean bite rate for a subset of the unprotected population. This involves a number of complications however, since accurate data would be required concerning bednet distribution and use, how this usage correlates to host infective state, and which proportion of bite are taken during the hours of sleeping.

There is a differential mean bite rate for hosts in the exposed, infected and recovered (EIR) individuals relative to the susceptible category (S), to produce over dispersive biting rates and reflect the fact that some individuals are more attractive to vectors [#!lindsay:93!#,#!knols:95!#,#!mukabana:02!#], are more vulnerable due to clothing and housing standards[#!lwetoijera:13!#], access to nets, location of housing with respect to water bodies [#!carter:00!#,#!bousema:12!#,#!kienberger:14!#], and that parasite infection also appears to increase attractiveness of individuals to vectors [#!lacroix:05!#], although the latter effect is offset by increased net use in the case of clinical symptoms. anthrophic vectors

The impact of using eqn. is to reduce the mean transmission rate, particularly when the mean bite rate is small resulting in a strong positive skewness of the Poisson distribution (Fig. 3). While this is an improvement on the simple assumption that all hosts receive equal numbers of bites, the Poisson distribution is likely under-dispersive compared to reality, since a number of factors such as unequal host attractiveness to vectors and nocturnal behaviour affecting exposure will likely lead to a uneven distribution of bites rates [#!dye:86!#,#!knols:95!#,#!mukabana:02!#]. Fig. 3 also emphasizes that the model is relatively insensitive to the choice of $P_{vh}$ for values exceeding around 0.2.

The host population is represented by the vector $H(N_{host})$ , and each VECTRI timestep a proportion $P_{v{\rightarrow}h}$ of hosts become infected and progress through the array until 20 days later they assume an infective status, an average value for immune and non-immune subjects [#!shute:51!#,#!miller:58!#,#!hawking:71!#,#!day:98!#]. Non-immune hosts clear infections at an e-folding rate of $C_{ni}=150$ days. Even after a century of study of the disease, the paradigm of naturally acquired immunity (NAI) is still hotly debated [#!doolan:09!#]. Therefore the present version of the model neglects host immunity, and the impact of the various representations of immunity in VECTRI will be the subject of a companion article.

PARAMETER TABLE