Larvae cycle

Previous laboratory studies have shown that the larvae growth rate follows the degree day concept [#!detinova:62!#] based on a linear function of water temperature $T_{wat}$ above a threshold value $T_{L,min}$ below which larvae growth ceases:

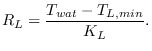$$R_{L}=\frac{T_{wat} - T_{L,min}}{K_{L}}.$$ (2)

There is considerable uncertainty in the setting of the rate coefficient $K_{L}$ , however, with [#!jepson:47!#] $K_{L}$ value of 90.9 degree days, while a linear approximation of the relationship derived by [#!bayoh:03!#] results in a much slower rate of 200 degree days. A further source of uncertainty is the specification of the water temperature itself, which depends on the shading of the pool and its dimensions in addition to the ambient air temperature, and is described in the hydrology component below. VECTRI also permits the user to avoid this uncertainty by following [#!ermert:11a!#] in setting a fixed larvae growth rate (i.e. independent of $T_{wat}$) to have a cycle of 12 days, the default option selected. The sensitivity to this relationship is investigated later. Irrespective of the scheme used, an upper temperature limit $T_{L,max}$ is specified above which larvae death occurs.

Figure: Larvae development rates as a function of temperature as modelled by [#!bayoh:03!#](black/red), [#!jepson:47!#](green) and [#!ermert:11a!#](blue). All three linear forms are implemented in VECTRI.

Egg hatching into larvae and the pupae development stage are both typically on the the order of one day [#!lyimo:92!#,#!bayoh:03!#] and thus are poorly resolved by the daily timestep employed by VECTRI and other similar dynamical models. In order to avoid truncation problems the length is fixed in VECTRI to last exactly one day and is temperature independent.