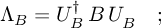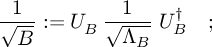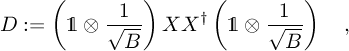2. Quantum Operations: The Hans-Jürgen algorithm
We are considering the Random Quantum Maps
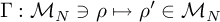 , ,
mapping the set 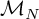 of N×N density matrices ρ in itself.
The Map Γ can be represented by a
N2×N2 matrix Φ, the so-called
Superoperator, which in turn can be reshuffled into a
positive and
Hermitian
N2×N2 dynamical matrix D of N×N density matrices ρ in itself.
The Map Γ can be represented by a
N2×N2 matrix Φ, the so-called
Superoperator, which in turn can be reshuffled into a
positive and
Hermitian
N2×N2 dynamical matrix D
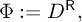 that is
that is
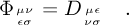 (1)
(1)
Other that positivity and
Hermiticity, another condition
must be fulfilled by D, for being a dynamical matrix
representing a quantum map Γ. This is the Trace
Preserving (TP) condition, namely
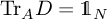 (2)
(2)
The Hans-Jürgen algorithm for producing a dynamical matrix D
consists in:
- generate a CPXL N2×N2 non Hermitian
matrix X drawn according to the Ginibre Unitary
Ensemble (the subroutine
GinUE.f
can be used for this purpouse);
- compute the N×N Hermitian matrix
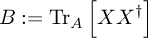
and diagonalize it, obtaining UB and
ΛB such that
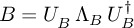 and
and
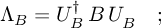
- use the latter decomposition for fixing the Hermitian matrix
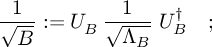
- compute the dynamical matrix
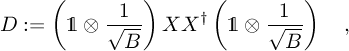
that now is positive, hermitian and fulfill eq. (2) by construction.
Once that one dynamical matrix D has been generated, the corresponding
superoperator Φ can be earned by eq. (1).
|
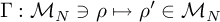 ,
,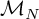 of N×N density matrices ρ in itself.
The Map Γ can be represented by a
N2×N2 matrix Φ, the so-called
Superoperator, which in turn can be reshuffled into a
of N×N density matrices ρ in itself.
The Map Γ can be represented by a
N2×N2 matrix Φ, the so-called
Superoperator, which in turn can be reshuffled into a
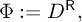 that is
that is
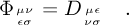
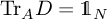
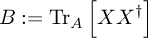
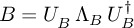 and
and